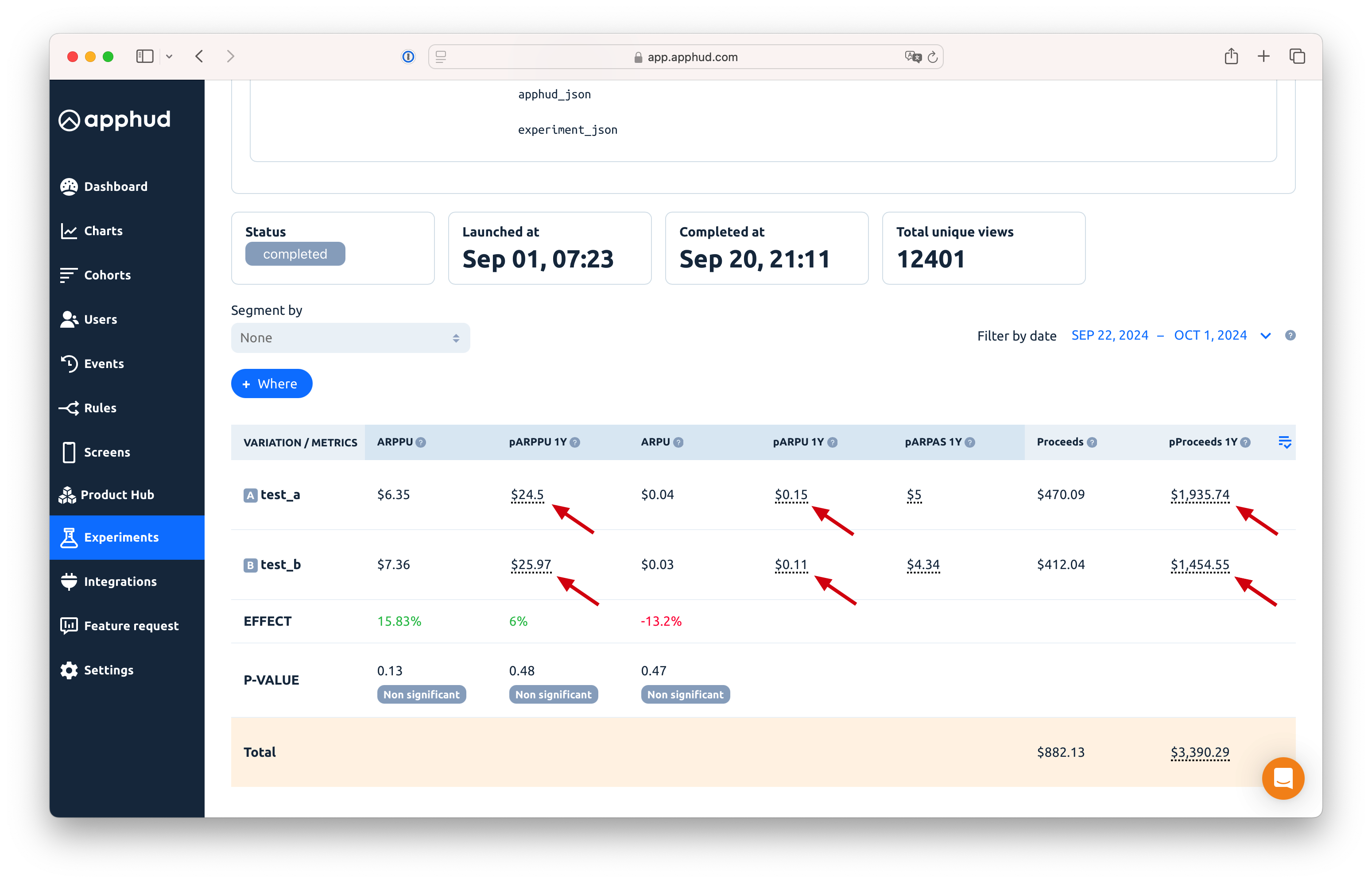
Experiment Predictions
Overview
A/B test predictions are structured similarly to the main predictions in LTV Predictions.
The following metrics help predict the results of experiment variations:
- pARPU 1Y
- pARPPU 1Y
- pARPAS 1Y
- pProceeds 1Y
Analyzing these predicted metrics is practically the same as analyzing their fact metrics: ARPU, ARPPU, ARPAS, Proceeds.
These predicted metrics are based on our approach to predicting the payback period.
Enable Predictions
Experiment Predictions are available if LTV Predictions feature has been added to your app. For more information on how to apply for predictions, follow this guide. If LTV Predictions are enabled for your app, just select these metrics from the metrics list.
Payback Period Calculation
Subscriptions are considered a contractual type of monetization, with purchases occurring at defined intervals (e.g., 1 week, 1 month). This creates various ways to define the payback period. The following example illustrates the complexity of defining the payback period:
We compare two subscriptions with these properties:
- Product 1: 3-month duration, non-trial, $20 price
- Product 2: 3-month duration, 7-day trial, $20 price
We aim to compare these subscriptions over a 1-year payback period.
The following table shows the predicted rebill rates:
| Product | Iteration | Predicted Rebill Rate | S(t) |
|---|---|---|---|
| product_1 | 0 | 1.000 | |
| product_1 | 1 | 1.526 | 52.63% |
| product_1 | 2 | 1.889 | 36.30% |
| product_1 | 3 | 2.169 | 27.92% |
| product_1 | 4 | 2.396 | 22.79% |
| product_2 | 0 | 1.000 | |
| product_2 | 1 | 1.600 | 60.00% |
| product_2 | 2 | 2.000 | 40.00% |
| product_2 | 3 | 2.286 | 28.57% |
| product_2 | 4 | 2.500 | 21.43% |
Consider that 100 subscriptions of product_1 were purchased. Here’s how the prediction plays out over days:
| Date | 2023-01-01 | 2023-01-01 | 2023-04-01 | 2023-06-30 | 2023-09-28 | 2023-12-27 | 2024-01-01 |
|---|---|---|---|---|---|---|---|
| Event | install | subscription_started (current iteration) | subscription_renewal (predict) | subscription_renewal (predict) | subscription_renewal (predict) | subscription_renewal (predict) | 1 year payback (starting from first paid transaction) |
| Iteration | - | 0 | 1 | 2 | 3 | 4 | (4) |
| Amount | 1000 | 100 | 52.6 | 36.3 | 28 | 22.7 |
For product_2, we get:
| Date | 2022-12-25 | 2023-01-01 | 2023-01-08 | 2023-04-08 - 2023-04-22 | 2023-04-22 | 2023-07-21 | 2023-10-19 | 2023-12-25 | 2024-01-01 | 2024-01-08 | 2024-01-17 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Event | install | trial_started | subscription_renewal | billing issue + grace period | subscription_renewal (current iteration) | subscription_renewal (predict) | subscription_renewal (predict) | 1 year payback (starting from install) | 1 year payback (starting from trial) | 1 year payback (starting from the first paid transaction) | subscription_renewal (predict) |
| Iteration | - | - | 0 | 1 | 2 | 3 | (3) | (3) | (4) | 4 | |
| Amount | 1000 | 400 | 100 | 60 | 40 | 28.6 | 21.4 |
As you can see, the prediction method differs based on the payback point used.
In LTV Predictions, it would appear as follows:
- Product 1:
pARPPU = (fact revenue (0) + predicted revenue (1, 2, 3, 4)) / paid subs = (100 * $20 + (52.6 + 36.3 + 28) * $20) / 100 = $47.92 - Product 2:
pARPPU = (fact revenue (0, 1) + predicted revenue (2, 3)) / paid subs = ((100 + 60) * $20 + (40 + 28.6) * $20) / 100 = $45.72
This calculation accounts for how many renewals are predicted within 365 days from the install date. However, this results in different iterations being used for predictions due to trial periods and delays.
To resolve this, we ignore the install date and 365-day limit and instead use the maximum iteration that can occur within the payback period. In this case, a 3-month subscription can generate up to 5 transactions (0 to 4 iterations) in 1 year. Thus, both products would predict up to the 4th iteration for A/B test predictions:
- Product 1:
pARPPU = (fact revenue (0) + predicted revenue (1, 2, 3, 4)) / paid subs = (100 * $20 + (52.6 + 36.3 + 28) * $20) / 100 = $47.92 - Product 2:
pARPPU = (fact revenue (0, 1) + predicted revenue (2, 3, 4)) / paid subs = ((100 + 60) * $20 + (40 + 28.6 + 21.4) * $20) / 100 = $50.00
Now, the products are comparable, and product_2 performs better.
This approach results in consistent lifetime iterations across products with the same duration. The table below shows iteration boundaries based on duration interval and lifetime:
| 1M | 3M | 6M | 1Y | |
|---|---|---|---|---|
| 1 week | 4 | 12 | 25 | 52 |
| 1 month | 1 | 2 | 6 | 12 |
| 2 month | 0 | 1 | 3 | 6 |
| 3 month | 0 | 1 | 2 | 4 |
| 6 month | 0 | 0 | 1 | 2 |
| 1 year | 0 | 0 | 0 | 1 |
Note 1: If an A/B test is conducted with one variation containing only trial subscriptions and the other only non-trial subscriptions, pARPAS is not a valid metric for comparison, so the p-value is not calculated for pARPAS.
Note 2: Optimizing solely for ARPPU does not always make sense when considering overall revenue. For example, if an A/B test splits traffic 50/50:
- Variation A: 1000 installs, 100 paid subscriptions, $40 pARPPU
- Variation B: 1000 installs, 200 paid subscriptions, $30 pARPPU
While Variation A seems better in terms of pARPPU, Variation B generates higher total revenue ($4000 < $6000). Hence, it’s useful to also consider pARPU and its p-value.
Updated 10 months ago
