Predictions
This guide describes LTV Predictions
Overview
Apphud offers advanced LTV prediction capabilities, providing valuable insights into future revenue streams for different customer cohorts. These predictions, based on historical data, are available for intervals of 30, 90, 180, and 365 days.
Understanding these forecasts is crucial for businesses to strategically allocate resources toward customer acquisition and retention.
Apply for Predictions
To access predictions:
Request Activation: Contact your support manager to request prediction features for your apps.
Initial Setup: Once requested, our team will activate the prediction functionality. Please allow at least 24 hours for the prediction model to be trained using your app's historical data.
Data Requirement: There are no strict data requirements. However, if there are no subscriptions with at least 2 conversions (except for a one-year subscription), basic predicted rebill rates are applied depending only on the duration interval (your application data is not used).
Availability of PredictionsCurrently, predictions are available for the following chart(s):
- Cumulative LTV chart
How it works
Our prediction model utilizes a sophisticated machine-learning algorithm to estimate the future value of each subscription:
Update Frequency: The model is updated daily and undergoes a full recalibration every week. This means that predictions for the current day's data will be available the following day.
Daily Update Time: The model updates at 00:00 UTC. If the latest data is not visible, please check back later.
Subscription Types: The model is particularly effective for weekly and monthly subscriptions.
Data Utilized: Predictions are based on various data points, including but not limited to:
- Purchase history
- Free trial data
- User demographics
In charts where predictions are present, a dashed line will indicate forecasted data. Users can adjust the cohort period (e.g., 180 or 365 days) for extended forecasts.
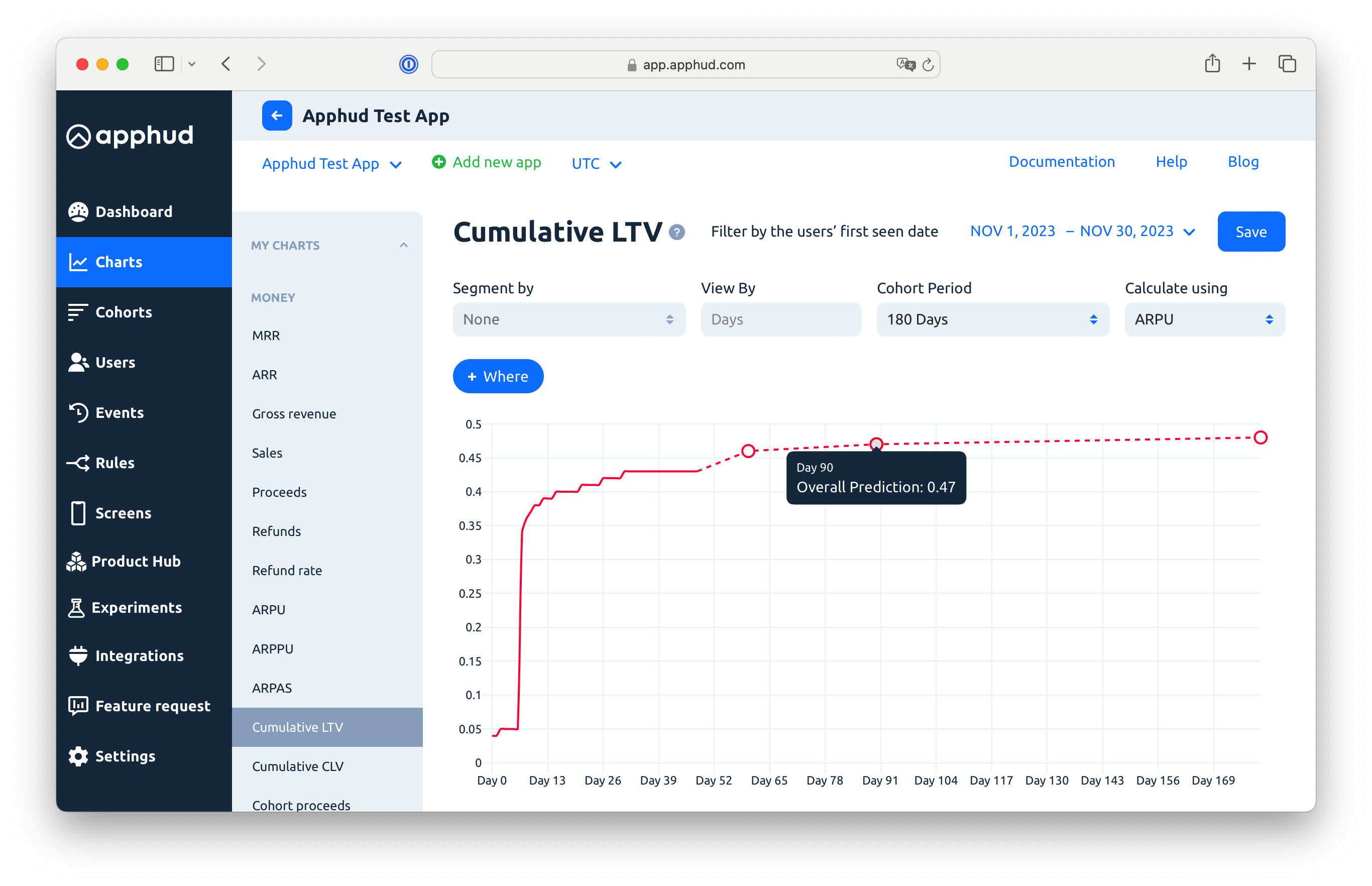
Predicted Dashed Line in Cumulative LTV Chart
The process of calculating subscriptions' forecasts includes the following pipelines:
- Model. This pipeline is intended to calculate predicted rebill rates over different segments using transactions history.
- Predictions. In this step, predicted rebill rates are applied for each subscription depending on the segment and current renewal iteration.
Model
Our model is considered to be a probabilistic model based on a history of churns/renewals.
It means that the model uses probability distribution to describe the funnel.
The main idea behind this approach is trying to find dependencies between metrics (retention rates, churn rates, rebill rates) over iterations in the way it could provide such parameters of probability distribution that maximize the likelihood of observed data. This can be shown with the example.
Assume that we have a 3-month subscription with the following funnel:
| Iteration | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Renewals | 200 | 80 | 50 | 35 |
0 iteration defines when the subscription started.
This funnel could be described with the following metrics:
| Iteration | Retention rate | Churn rate | Rebill rate |
|---|---|---|---|
| 0 | 1 | ||
| 1 | 40% | 60% | 1.4 |
| 2 | 62.5% | 15% | 1.65 |
| 3 | 70% | 7.5% | 1.825 |
These metrics could be associated with functional characteristics of discrete random variable:
- retention rate ~ reverse of hazard function
h(p, t) - churn rate ~ probability mass function
P(p, t) - rebill rate ~ cumulative survival function
S(p, i)
Considering these assumptions we can find parameters p of probability distribution using maximum likelihood estimation.
The result of estimation is such a parameter that most likely gives observed data and allows us to predict metrics of unobserved iterations.
There are many different probability distributions that could be applied for this purpose, but we use the shifted Beta-Geometric (sBG) model, which is considered to be the most common model for discrete-time subscription-based data.
Applying the sBG model to the data above, we get the following results:
| Iteration (t) | Retention rate (1-h(t)) | Churn rate (P(t)) | Rebill rate (sum(S(i)) |
|---|---|---|---|
| 0 | 1 | ||
| 1 | 40.10% | 59.90% | 1.401 |
| 2 | 61.34% | 15.50% | 1.647 |
| 3 | 71.46% | 7.02% | 1.823 |
| 4 | 77.38% | 3.98% | 1.959 |
| 5 | 81.27% | 2.55% | 2.069 |
| 6 | 84.02% | 1.77% | 2.162 |
| 7 | 86.06% | 1.29% | 2.242 |
| 8 | 87.64% | 0.99% | 2.312 |
Starting from the 4th iteration we have predicted rebill rates.
Mathematically inclined readers who are interested in a more detailed description of the logic and algorithms behind the sBG model could refer to the article Fader P. S. & Hardie B. G. S. "How to project customer retention".
Segmentation
The algorithm described before allows us to calculate predicted rebill rates on specific segment.
However, there are some restrictions over segments that make impossible to estimate model parameters:
- a segment has too short funnel
- a segment has not enough subscriptions
- a segment has no consistent data
This development implies that we need to use calculation over a cascade of segments on different levels and subsequently hierarchically apply them when making predictions.
The following example demonstrates how data could be calculated. Assume a cascade is represented like this:
duration_interval
duration_interval, app_id
duration_interval, app_id, is_trial
duration_interval, app_id, is_trial, country_tier
As a result, we keep values of predicted rebill rates over a cascade of segments:
| duration_interval | app_id | is_trial | country_tier | predicted_rebill_rate (1 year payback) |
p |
|---|---|---|---|---|---|
... |
... |
... |
... |
... |
... |
1 month |
overall |
overall |
overall |
4.5 |
(3.5, 5.6) |
... |
... |
... |
... |
... |
... |
1 week |
id1234567890 |
overall |
overall |
7.9 |
(4.3, 1.6) |
... |
... |
... |
... |
... |
... |
1 year |
id1111111111 |
true |
overall |
1.3 |
(2.5, 3.0) |
... |
... |
... |
... |
... |
... |
3 month |
id6666666666 |
false |
US |
2.3 |
(0.5, 1.7) |
... |
... |
... |
... |
... |
... |
If subscription properties have no matched predicted rebill rate on some level then it takes value from the higher level and so on.
A cascade allows making predictions for any subscription and at the same time keeping accuracy if it is possible.
Note: p contains parameters of the probability distribution that describe the funnel: retention rates, churn rates, etc.
Predictions
As we have a cascade of segments, we can calculate predictions for any subscription with the following steps:
- Determine if the subscription is active. If not, predictions aren't applied.
- Try to find a model within the cascade of segments that matches by properties as closely as possible.
- Determine what the last iteration of the subscription is.
- Apply the model depending on the current iteration, and store the fee, VAT, and price.
Note: This mechanism is called a dynamical prediction. This means that as the subscription renews, the prediction updates.
Note: An active subscription is assumed to have an expiration date greater than today. Even if the subscription was canceled but not expired, predictions are applied. Otherwise, it leads to underestimation.
Note: If the subscription is active but in a trial period, predictions are also calculated in the same way, applying a trial conversion rate that comes from historical data.
Best Practices for Usage
Date Range Selection: Opt for broader date ranges for more accurate predictions. However, avoid overly extensive periods.
Filter Usage: Limit the depth of the filter application as it can reduce the cohort data size, affecting prediction accuracy.
Volume Consideration: For apps with high daily transaction volumes, shorter date ranges, even a day, can be effective. Conversely, for lower volumes, choose intervals covering at least 200 subscribers for better accuracy.
Privacy and Data Use
Anonymity: Data utilized for predictions is anonymous and specific to each app, ensuring privacy and data integrity.
Aggregated Data: In scenarios with insufficient historical data, aggregated anonymous data at the overall level may be used to enhance prediction accuracy.
Updated 10 months ago
